卷积神经网络LeNet5

本文使用LeNet5识别手写数字。

LetNet-5 的基本结构

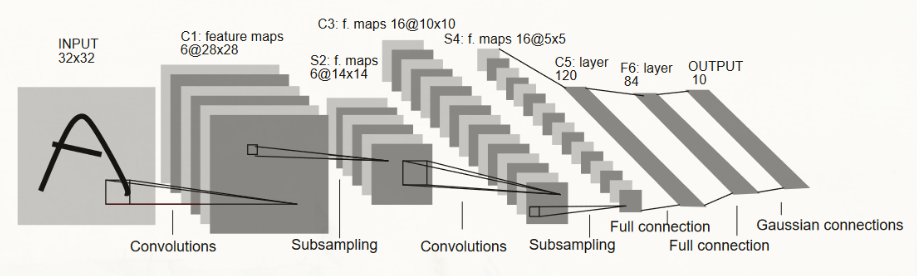
LeNet-5包含7层网络结构（不含输入层），包含两个卷积层、两个降采样层（池化层）、两个全连接层和输出层。

1.输入层(input layer)

输入层的大小为32×32手写图像，在实际应用中，通常会对图像进行预处理，如对像素进行归一化。

2、卷积层C1（Convolutional layer C1）

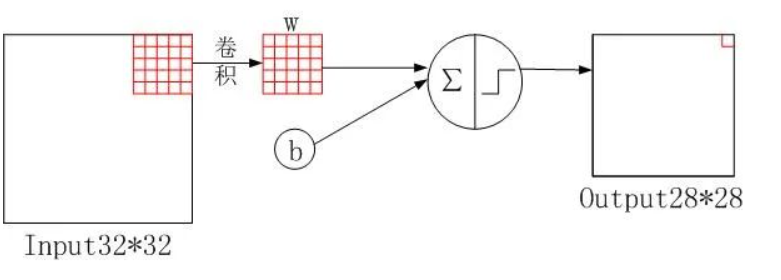
代码：

1	`nn.Conv2d(1, 6, kernel_size=5, padding=2)`

根据代码的含义，通道数从1变6，原图的尺寸从32×32变为28×28，这与卷积核大小、步幅和$padding$有关，其输出的特征图像尺寸如下：
$$
output size = \frac{W-kernelsize+2×padding}{stride}+1
$$
其中，$W$表示输入图像的宽度。
$$
output size = \frac{32-5+2×0}{1}+1 = 28
$$
代码：

1	`nn.Sigmoid()`

在卷积操作完成之后会进行归一化（Batch Normalization）操作提高神经网络和加速收敛

3、采样层S2（Subsampling layer S2）

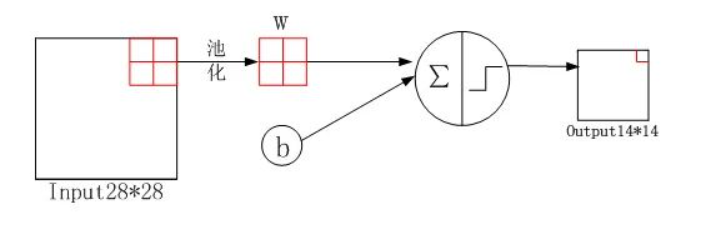
代码：

1	`nn.Conv2d(6, 16, kernel_size=5)`

通道数没有发生过改变，计算公式如下：
$$
outputsize =\frac{W-poolsize}{stride}+1 = \frac{28-2}{2}+1 = 14
$$
然后同上，进行批量归一化。

4、卷积层C3（Convolutional layer C3）

代码：

1	`nn.Conv2d(6, 16, kernel_size=5)`

通道数由6变16，输出特征图尺寸为10x10，具体计算如下：
$$
output size = \frac{W-kernelsize+2×padding}{stride}+1 = \frac{14-5+2×0}{1}+1 = 10
$$
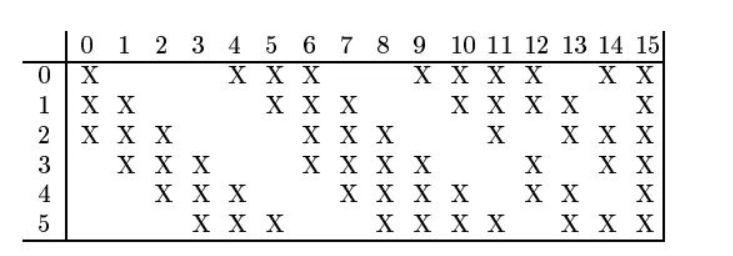
该层较为特殊，16 个卷积核并不是都与 S2 的 6 个通道层进行卷积操作，如下图所示，C3 的前六个特征图（0,1,2,3,4,5）由 S2 的相邻三个特征图作为输入，对应的卷积核尺寸为：5x5x3；接下来的 6 个特征图（6,7,8,9,10,11）由 S2 的相邻四个特征图作为输入对应的卷积核尺寸为：5x5x4；接下来的 3 个特征图（12,13,14）号特征图由 S2 间断的四个特征图作为输入对应的卷积核尺寸为：5x5x4；最后的 15 号特征图由 S2 全部(6 个)特征图作为输入，对应的卷积核尺寸为：5x5x6。

5、采样层S4（Subsampling layer S4）

代码：

1	`nn.AvgPool2d(kernel_size=2, stride=2),`

特征图尺寸由10×10变成5×5，输出通道还是16。
$$
outputsize = \frac{W-kernelsize}{stride}+1 = \frac{10-2}{2} +1 = 5
$$

6、全连接层C5（Fully connected layer C5）

代码：

1	`nn.Linear(16 * 5 * 5, 120)`

C5将每个大小为 5×5 的特征图拉成一个长度为400**(维度为1X16X5X5)**的向量，并通过一个带有120个神经元的全连接层进行连接。120是由LeNet-5的设计者根据实验得到的最佳值。

7、全连接层F6（Fully connected layer F6）

全连接层F6将120个神经元连接到84个神经元。

8、输出层（Output layer）

输出层由10个神经元组成，每个神经元对应0-9中的一个数字，并输出最终的分类结果。

搭建网络

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

加载数据集

# 加载训练集
train_dataset = torchvision.datasets.MNIST(root = './data',	# 数据集保存路径
                                           train = True,	# 是否为训练集
                                           # 数据预处理
                                           transform = transforms.Compose([
                                                  transforms.Resize((32,32)),
                                                  transforms.ToTensor(),
                                                  transforms.Normalize(mean = (0.1307,), 
												                     std = (0.3081,))]),
                                           download = True)	#是否下载
 
# 加载测试集
test_dataset = torchvision.datasets.MNIST(root = './data',
                                          train = False,
                                          transform = transforms.Compose([
                                                  transforms.Resize((32,32)),
                                                  transforms.ToTensor(),
                                                  transforms.Normalize(mean = (0.1325,), 
												                     std = (0.3105,))]),
                                          download=True)
# 一次抓64张牌
batch_size = 64
# 加载训练数据
train_loader = torch.utils.data.DataLoader(dataset = train_dataset,
                                           batch_size = batch_size,
                                           shuffle = True)	# 是否打乱
# 加载测试数据
test_loader = torch.utils.data.DataLoader(dataset = test_dataset,
                                           batch_size = batch_size,
                                           shuffle = False)	# 是否打乱

测试阶段的shuffle=False：在测试阶段，通常不需要打乱数据的顺序。测试时模型是在未见过的数据上进行评估，因此希望模型看到的是原始数据的有序顺序，以便能够更好地评估模型的泛化性能。如果在测试时也打乱数据，可能会导致模型在评估时看到的数据分布与实际场景不一致。（其实如果是True影响也不大）

设置评价指标

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

模型训练

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],legend=['train loss', 'train acc', 'test acc'])此代码为绘制折线图
以上代码个 epoch 结束时都会计算并得到一次测试集的准确率，并将其记录下来

最终得到训练结果

1 2	`lr, num_epochs = 0.9, 10 train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())`

1 2	`loss 0.469, train acc 0.823, test acc 0.779 55296.6 examples/sec on cuda:0`

深度学习基础

卷积神经网络LeNet5

http://example.com/2024/11/11/卷积神经网络LeNet/

作者

yzcabe

发布于

2024年11月11日

许可协议

循环神经网络上一篇

张量的基本操作下一篇